Cours du 13/04
Bonjour, hier nous avons continué le chapitre sur les nombres complexes, ainsi je vous fais part de la leçon assez détaillé pour ceux qui n’étaient pas là et de divers petits astuces pour toute la classe.
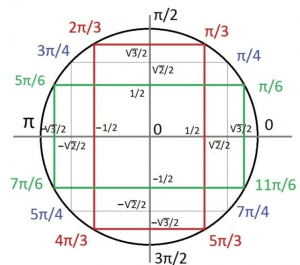
Pour la suite de ce chapitre il sera nécessaire de connaitre le cercle trigonométrique, voici un petit rappel
Avant de passer au grand II de la leçon, nous pouvons retenir que le module est une longueur et se note |z| et l’argument est un angle et se note arg(z). (Arg(z)=/2 + 2k)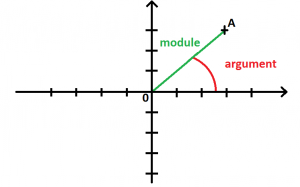
Dans un premier temps nous avons vu les propriétés sur les modules et arguments (II) On appelle module du nombre complexe z = x+iy le réel positif , le module est donc toujours positif. Il faudra alors retenir que pour calculer le module on utilisera |z|=√(x2+y2).
Puis nous avons étudié différentes propriétés et démonstrations sur les modules puis sur l’argument.
a) Sur les modules
Soient z1 et z2 appartient à C. |z1z2|=|z1|*|z2|.
Si z2 différent de 0. |1/z2|=1/z2
Démo : Soit z1=x+iy x,y,x’ et y’ appartiennent à R
z2=x’+iy’
1) |z1*z2|= (xx’-yy’) + i(xy’-x’y) =√((xx’-yy’)2+(xy’+x’y)2) z1|*|z2|= √(x2+y2)*√(x’2+y’2)=√(x^2*x’^2+y^2*y’^2+x^2*y’^2+x’^2*y^2)=√((x^2+y^2)+(x’^2+y’^2))
2) 1/|z2|= 1/√(x’^2+y’^2)
|1/z2 |= z2barre/z2*z2barre= x’-y’i/z2barre=√((x’^2+y’^2) / (|z|^2)^2)= |z2|/|z2|^2=1/|z2|
Afin d’établir la troisième démonstration il faudra s’aider de la première ainsi que de la deuxième pour |z1/z2 |.
Nous retiendrons que pour tout z appartenant à C : |z|=|-z|=| /z|= |-/z|
b) Sur l’argument Propriété: Soit z appartenant à C* et z’ appartenant à C*
1) arg(z*z’)=arg(z)+arg(z’) modulo 2pi
2) arg(1/z)= -arg(z’) modulo 2pi
3) arg(z/z’)=arg(z)-arg(z’) modulo 2pi
Ici, les propriétés sur l’argument peuvent nous rappeler les propriétés algébriques de l’exponentielle, cela pourrait vous aider comme petit moyen mémo technique.
Voici la démonstration : r et r’ appartenant à R
1) Soit z = r (cos(alpha)+isin(alpha))
z’ = r’(cos(alpha’)+isin(alpha’))
zz’= rr’ (cos(alpha)+isin(alpha)) (cos(alpha’)+isin(alpha’)) = rr’(cos(alpha)*sin(alpha’)-sin(alpha)*sin(alpha’)+i(cos(alpha)*sin(alpha’)+sin(alpha)*cos(alpha’))= rr'(cos(alpha+alpha’)+isin(alpha+alpha’))
rr’>0 donc arg(zz’)= apha + alpha’ modulo 2pi =arg(z)+arg(z’)
Enfin nous avons vu la forme exponentielle qui nous permet de simplifier : cos(alpha)+isin(alpha)= exp^(i(alpha) (c’est juste une notation de simplification car il n’y a pas de nombres complexes dans la fonction exponentielle)
Pour tout alpha appartenant à R exp^(i(alpha)*exp(i(beta)=exp^(i(alpha+beta) exp^(i(alpha))/exp(i(beta))=exp^(i(alpha-beta)
Propriété: On doit savoir que si |zA| = r, arg(z) = θ, on a alors : z =r exp^(i(teta)) c’est la forme exponentielle de z.

Bonjour.
Merci pour ton article Mahina. Le cour est très bien rédiger. Les propriété sont assez simple, pour d’éventuelle oublie ils suffit de reprendre ceux de l’exponentiel. Je voudrais rajouter qu’après le calcule du module, pour calculer l’argument, dans certain cas, ne pas oublier de passer par le calcule du cosinus de l’angle téta : Cos = x/|z| et du sinus de l’angle téta : Sin = y/|z|. X et Y que nous reprenions dans le module z=x+iy.
Pour par la suite s’aider du cercle du cercle trigo pour trouver la valeur de l’argument en faisant correspondre le cosinus et le sinus, d’où l’importance du cercle trigo.
Bonne soirée @+